DARING KELAS 10 MIPA MATEMATIKA PEMINATAN MATERI OPERASI HITUNG VEKTOR PADA BIDANG

 

B. Operasi Vektor

1. Penjumlahan vector secara geometris

Dari ketiga vector tersebut dapat dijumlahkan dengan cara sebagai berikut:

Pada penjumlahan vector berlaku hukum

a + b = b + a

Pada vector berlaku sifat ASOSIATIF

(a + b) + c = a + (b + c)

2. Pengurangan vector secara geometris

Pengurangan vector dapat dilakuakan dengan menjumlahkan vector 1 dengan lawan vector 2.

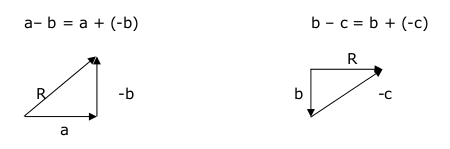
3. Penjumlahan dan pengurangan vector secara analisis

Untuk menjumlahkan vector-vektor 3 dimensi digunakan metode analitik.

Penguraian vector :

Vector a dapat diuraikan menjadi Ax dan Ay

Ax = a cos θ

Ay = a sin θ

Utuk menentukan besarnya vector a dan arah vector a dapat digunakan rumus sebagai berikut:

C. Perkalian Vektor

1. Perkalian sebuah konstanta dengan sebuah vektor

• “Jika k positif maka arahnya sama dengan arah vector a”
• “Jika k negatif maka arahnya berlawanan dengan vector a”

2. Perkalian dua buah vector dengan hasil berupa skalar

Operasi di atas disebut juga “dot product”

Keterangan:

a = vector a

b = vector b

θ = sudut yang dibentuk antara vector a dan vector b

3. Perkalian dua buah vector dengan hasil berupa vector lain

Keterangan:

a = vector a

b = vector b

θ = sudut yang dibentuk antara vector a dan vector b

Operasi di atas disebut juga “cross product”

Arah hasil perkalian vector a dan b selalu tegak lurus dengan bidang yang dibentuk oleh vector a dan b.

Untuk menentukan arah perkalian vector:

Kepalkan jari tangan melingkupi sumbu sambil mendorong vector a ke vector b oleh ujung-ujung jari melalui sudut terkecil, sementara ibu jari tetap tegak jadi hasil perkalian vector a dan b ditentukan oleh ibu jari.

Jika kita mengetahui komponen-komponen vector yang akan kita kalikan, kita bisa menggunakan sifat-sifat perkalian silang diantara sesama vector satuan untuk mencari hasil perkalian silang antara dua vector. Sifat-sifat tersebut adalah:

i x i = j x j = k x k = 0

i x j = -j x i = k

j x k = -k x j = i

k x i = -i x k = j

dengan sifat-sifat tersebut kita peroleh :

A x B = (Ax i + Ay j + Az k) x (Bx i + By j + Bz k)

A x B = (Ay Bz - A z By )i + (A z BX - Ax BZ )j +(Ax By - Ay Bx )k

Berarti jika C = A x B, maka komponen-komponen dari C sama dengan :

C = Cx I + Cy j + Cz k adalah :

Cx = Ay Bz - Az By

Cy = Az BX - Ax BZ

Cz = Ax By - Ay Bx

LATIHAN 

MENGERJAKAN LKS HALAMAN 21 NO 2 DIKERJAKAN SETELAH ITU DIFOTO DAN DIKIRIM KE WA BU HANUM