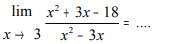DARING KELAS 11 TGL 15 FEBRUARI 2022 MATEMATIKA WAJIB BAB LIMIT FUNGSI

 

Pengertian Limit Fungsi Aljabar – Materi Limit Matematika Kelas 11

Sebelum mulai memahami konsep dengan lebih mendalam tentang materi limit Matematika dan mencoba menyelesaikan contoh soal limit fungsi aljabar, elo harus memahami pengertiannya dulu.

Nah, limit adalah suatu nilai yang menggunakan pendekatan fungsi saat mendekati nilai tertentu. Kalau bahasa sederhananya, limit dapat dikatakan sebagai nilai yang menuju suatu batas, batas yang bisa dikatakan dekat namun tidak bisa dicapai. 

Illustrasi materi limit Matematika (Dok. shutterstock.com)

Kok tetep ribet ya? Hehehe… Kalau gitu, coba lihat konsep atau bentuk umum dari limit fungsi di bawah ini:

Limit f(x) mendekati c sama dengan L, ditulis:

jika untuk setiap x yang cukup dekat dengan c tetapi x≠c, f(x) mendekati L.

Gimana? Sudah ada bayangan belum mengenai pengertian limit fungsi aljabar?

Nah, setelah elo mengetahui pengertian limit fungsi aljabar, selanjutnya yang tak kalah penting adalah elo harus paham terhadap sifat-sifat limit. Sifat-sifat ini akan berguna saat elo menentukan nilai suatu limit nantinya. 

Sifat-Sifat Limit Fungsi

Seperti yang gue jelaskan sebelumnya, sifat-sifat limit fungsi dalam materi limit kelas 11 sangat penting untuk dipahami karena akan berguna sebagai bekal atau dasar saat elo mencari nilai suatu limit dalam soal-soal. Jadi, untuk memahami dengan benar setiap sifatnya bisa elo lakukan saat mengerjakan latihan soal. 

Sifat-sifat limit fungsi aljabar ditentukan jika n adalah bilangan bulat positif, k konstanta, f dan g adalah fungsi-fungsi yang memiliki limit di c, maka selanjutnya berlaku teorema-teorema berikut:

Oke, jadi itu beberapa sifat-sifat limit fungsi dalam materi limit Matematika kelas 11 yang perlu dan penting banget untuk elo pahami. Selanjutnya, gue akan menjelaskan mengenai cara mencari nilai limit fungsi.

Mencari Nilai Limit Fungsi

Setelah mengetahui apa saja sifat dari limit, selanjutnya dalam materi limit Matematika, ada cara mencari nilai limit fungsi yang bisa dilakukan menggunakan 3 metode, yaitu metode substitusi, pemfaktoran, dan mengalikan dengan faktor sekawan. 

Berikut gue jelaskan dengan lebih lanjut mengenai ketiga metode tersebut lengkap dengan contoh soal limit fungsi aljabar dan pembahasannya. 

Metode Substitusi

Metode substitusi merupakan cara yang paling dasar untuk mencari nilai limit. Metode ini dilakukan dengan mensubstitusi langsung nilai kedalam fungsi f(x).

Contoh Soal:

Metode Pemfaktoran

Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:

maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian baru bisa disubstitusikan.

Contoh Soal:

Metode Mengalikan dengan Faktor Sekawan

Jika pada metode substitusi menghasilkan nilai limit yang irasional, maka fungsi dikalikan dengan akar sekawannya, kemudian bisa disubstitusikan.

Contoh Soal:

LATIHAN 

1. Tentukan :
 

2. Tentukan :

jawabannya kirim ke wa bu hanum 

DARING KELAS 11 MATEMATIKA WAJIB TGL 31 AGUSTUS 2021 MATERI PROGRAM LINEAR

 

Program Linear

Program linear adalah suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimal atau minimum) diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear. Di dalam persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear.

Lihat juga materi StudioBelajar.com lainnya:
Persamaan Lingkaran
Trigonometri

Model Matematika Program Linear

Persoalan dalam program linear yang masih dinyatakan dalam kalimat-kalimat pernyataan umum, kemudian diubah kedalam model matematika. Model matematika merupakan pernyataan yang menggunakan peubah dan notasi matematika.

Sebagai ilustrasi, produsen sepatu membuat 2 model sepatu menggunakan 2 bahan yang berbeda. Komposisi model pertama terdiri dari 200 gr bahan pertama dan 150 gr bahan kedua. Sedangkan komposisi model kedua terdiri dari 180 gr bahan pertama dan 170 gr bahan kedua. Persediaan di gudang bahan pertama 72 kg dan bahan kedua 64 kg. Harga model pertama adalah Rp. 500.000,00 dan model kedua Rp. 400.000,00. Jika disimpulkan/disederhanakan dalam bentuk tabel menjadi berikut:

Dengan peubah dari jumlah optimal model 1 adalah x dan model 2 adalah y, dan hasil penjualan optimal adalah f(x, y) = 500.000x + 400.000y. Dengan syarat:

• Jumlah maksimal bahan 1 adalah 72.000 gr, maka 200x + 180y ≤ 72.000.
• Jumlah maksimal bahan 2 adalah 64.000 gr, maka 150x + 170y ≤ 64.000
• Masing-masing model harus terbuat.

Model matematika untuk mendapat jumlah penjualan yang maksimum adalah:

Maksimum f(x, y) = 500.000x + 400.000y

Syarat:

• 200x + 180y ≤ 72.000
• 150x + 170y ≤ 64.000
• x ≥ 0
• y ≥ 0

Yuk belajar materi ini juga:
Jaringan Tumbuhan
Teks Ceramah
Gerund and Infinitive

Nilai Optimum Fungsi Objektif

Fungsi objektif merupakan fungsi linear dan batasan-batasan pertidaksamaan linear yang memiliki himpunan penyelesaian. Himpunan penyelesaian yang ada merupakan titik-titik dalam diagram cartesius yang jika koordinatnya disubstitusikan kedalam fungsi linear dapat memenuhi persyaratan yang ditentukan.

Nilai optimum fungsi objektif dari suatu persoalan linear dapat ditentukan dengan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya dapat ditentukan letak titik yang menjadi nilai optimum. Langkah-langkahnya sebagai berikut :

• Menggambar himpunan penyelesaian dari semua batasan syarat yang ada di cartesius.
• Menentukan titik-titik ekstrim yang merupakan perpotongan garis batasan dengan garis batasan yang lainnya. Titik-titik ekstrim tersebut merupakan himpunan penyelesaian dari batasannya dan memiliki kemungkinan besar membuat fungsi menjadi optimum.
• Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu :
  • Menggunakan garis selidik
  • Membandingkan nilai fungsi objektif tiap titik ekstrim

Menggunakan Garis Selidik

Garis selidik diperoleh dari fungsi objektif f(x, y) = ax + by dimana garis selidiknya adalah

ax + by = Z

Nilai Z diberikan sembarang nilai. Garis ini dibuat setelah grafik himpunan penyelesaian pertidaksamaan dibuat. Garis selidik awal dibuat di area himpunan penyelesaian awal. Kemudian dibuat garis-garis yang sejajar dengan garis selidik awal. Berikut pedoman untuk mempermudah penyelidikian nilai fungsi optimum:

Cara 1 (syarat a > 0)

• ika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kiri garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.

Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kanan garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.

Cara 2 (syarat b > 0)

• Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di bawah garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
• Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di atas garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.

Untuk nilai a < 0 dan b < 0 berlaku kebalikan dari kedua cara yang dijelaskan di atas.

Membandingkan Nilai Fungsi Tiap Titik Ekstrim

Menyelidiki nilai optimum dari fungsi objektif juga dapat dilakukan dengan terlebih dahulu menentukan titik-titik potong dari garis-garis batas yang ada. Titik-titip potong tersebut merupakan nilai ekstrim yang berpotensi memiliki nilai maksimum di salah satu titiknya.

Berdasarkan titik-titik tersebut ditentukan nilai masing-masing fungsinya, kemudian dibandingkan. Nilai terbesar merupakan nilai maksimum dan nilai terkecil merupakan nilai minimum.

Yuk belajar materi ini juga:
Kesetimbangan Benda Tegar
Termokimia
Momen Inersia

Contoh Soal Program Linear dan Pembahasan

Contoh Soal 1

Tentukan nilai minimum f(x, y) = 9x + y pada daerah yang dibatasi oleh 2 ≤ x ≤ 6, dan 0 ≤ y ≤ 8 serta x + y ≤ 7.

Pembahasan 1:

• Langkah 1 menggambar grafiknya

• Langkah 2 menentukan titik ekstrim

Dari gambar, ada 4 titik ekstrim, yaitu: A, B, C, D dan himpunan penyelesaiannya ada di area yang diarsir.

• Lankah 3 menyelidiki nilai optimum

Dari grafik diketahui titik A dan B memiliki y = 0, sehingga kemungkinan menjadi nilai minimum. Kedua titik disubstitusikan kedalam f(x, y) = 9x + y untuk dibandingkan.

Dengan membandingkan, disimpulkan titik A memiliki nilai minimum 18

Contoh Soal 2

Tentukan dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!

Pembahasan 2:

Titik ekstrim pada gambar adalah:

• A tidak mungkin maksimum karena titik paling kiri.
• B(3, 6)
• C(8, 2)
• D(8, 0)

Nilai tiap titik ekstrim adalah:

• 
• 
• 

Sehingga nilai maksimum ada pada titik yang melalui garis BC dengan nilai maksimum 42.

Contoh Soal 3

Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.

Pembahasan 3:

Diketahui:

  

360p geselecteerd als afspeelkwaliteit

Dengan syarat:

• Kapasitas tempat: x + y ≤ 400
• Modal: 4.000x + 1.600y ≤ 1.000.000 
• x ≥ 0
• y ≥ 0

Diagramnya:

Titik ekstrim:

• A(0, 400) bukan optimum karena tidak ada apel
• C(250, 0) bukan optimum karena tidak ada pisang
•  dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:

• Apel: 150 kg
• Pisang: 250 kg

HARI INI TIDAK ADA TUGAS CUMAN MATERI DI ATAS DIPAHAMI

DARING KELAS 11 MATEMATIKA WAJIB TGL 24 AGUSTUS 2021 MATERI PENERAPAN INDUKSI MATEMATIKA

 

Bentuk Penerapan Induksi Matematika

Dalam belajar materi induksi matematika kita harus mengetahui juga penerapan dari induksi matematika. Beberapa penerapan induksi matematika yaitu pada penerapan induksi matematika barisan bilangan, penerapan induksi matematika pada keterbagian, dan penerapan induksi matematika pada ketidaksamaan (ketaksamaan). Untuk lebih memahaminya, perhatikan contoh soal berikut ini.

Contoh Soal dan pembahasan penerapan induksi matematika

Untuk n bilangan asli, x ≠ 1, buktikan dengan induksi matematika bahwa xⁿ – 1 habis dibagi (x – 1).

Pembahasan:

Misalkan P(n) = xn – yn .

Untuk membuktikan P(n) = xⁿ – 1 habis dibagi (x  –  1), artinya P(n) dapat dituliskan sebagai kelipatan x – 1.

Oleh karena itu, akan ditunjukkan P(n) = xⁿ – 1 memenuhi kedua prinsip induksi matematika.

 

Langkah Awal :

Untuk n = 1, sangat jelas bahwa x – 1 = (x – 1) × 1.

Demikian halnya untuk n = 1 diperoleh bahwa x² – 1 = (x – 1)(x + 1). Artinya jelas bahwa P(2) = x² – 1 habis dibagi (x – 1).

 

Langkah Induksi :

Pada bagian langkah induksi, kita peroleh bahwa P(2) benar. Karena P(2) benar, maka P(3) juga benar. Namun, perlu kita selidiki pola hasil bagi yang diperoleh untuk n pangkatt 3.

• Untuk n = 3, maka x³ – 1 = (x – 1)(x² + x + 1 ).
• Untuk n = 4, maka x⁴ – 1= (x – 1)(x³ + x² + x + 1).
• Untuk n = 5, maka x⁵ – 1 = (x – 1)(x⁴ + x³ + x² + x + 1).

Jadi untuk n = k, maka P(k) = x^k – 1 = (x – 1)(x^{k – 1} + 1).

Oleh karena itu, disimpulkan bahwa P(k) = x^k – 1 habis dibagi x – 1. Selain itu, juga dapat kita simpulkan bahwa P(k – 1) = x^{k – 1} – 1 juga habis dibagi (x – 1).

Contoh Soal Induksi Matematika

Contoh soal induksi matematika terdiri dari soal induksi matematika dan pembahasan induksi matematika. Berikut 3 Contoh Soal Induksi Matematika

1. Buktikan bahwa pernyataan berikut ini adalah salah. Jika n bilangan asli, maka terdapat paling sedikit satu bilangan prima p sedemikian sehingga n < p < n + 3.

Pembahasan Induksi Matematika

Pembuktian secara langsung :

Misalkan n = 19, maka n + 3 = 22

Ternyata tidak berlaku 19 < p < 22 karena tidak ada bilangan prima antara 19 dan 22.

 

2. Salah satu faktor dari n³ – 1 adalah 1, n bilangan asli.

Pembahasan Induksi Matematika

Pembuktian secara langsung:

n³ – 1 = (n – 1)( n² + n + 1), di mana n = 1.

Jadi terbukti bahwa salah satu faktor dari n³ – 1 adalah 1.

 

3. Diberikan a > 2, buktikan aⁿ > 0, n bilangan bulat positif.

Pembahasan Induksi Matematika

Langkah Awal :

Untuk a > 2, sangat jelas bahwa aⁿ > 0

Demikian halnya untuk a = 3 diperoleh bahwa 3ⁿ > 0. Artinya jelas bahwa P(2) = 3² > 0

 

Langkah Induksi :

Pada bagian langkah induksi, kita peroleh bahwa P(2) benar. Karena P(2) benar, maka P(3) juga benar. Namun, perlu kita selidiki pola hasil bagi yang diperoleh untuk n pangkatt 3.

• Untuk n = 3, maka 3³ = 27 > 0.
• Untuk n = 4, maka 3⁴ = 81 > 0
• Untuk n = 5, maka 3⁵ = 273 > 0

Jadi untuk n = k, maka P(k) = 3^k > 0.

Oleh karena itu, disimpulkan bahwa P(k) = a^k – 1 > 0. Selain itu, juga dapat kita simpulkan bahwa P(k – 1) = a^{k – 1} > 0.

hari ini tidak ada tugas tetapi kalian pahami materi di atas dan jangan lupa mengisi absen di grup

terimakasih